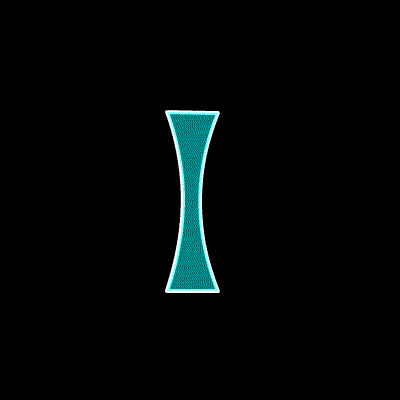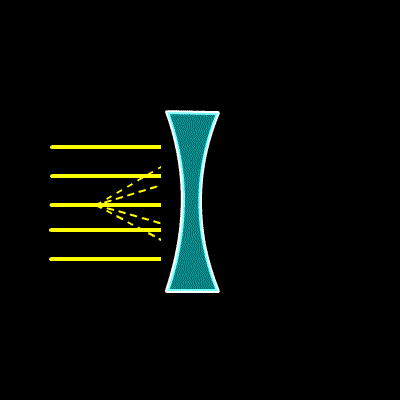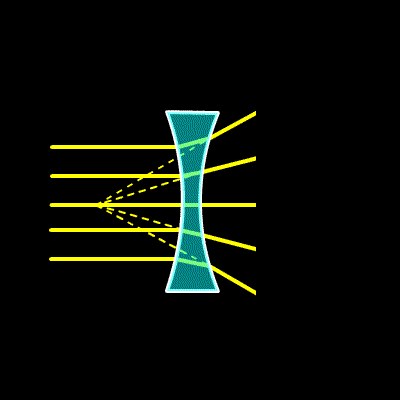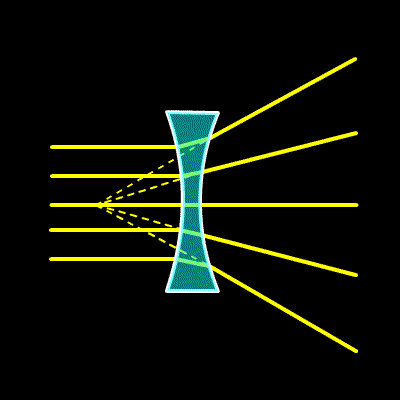In order to understand how lenses work, we need to clarify some difficult science first. To determine the path of a ray of light, we normally use vectors. If we want to show light going from point A to point B, then this vector is a single line (the reality is not like that, but we use this to simplify the process for those not in the know).
Now the difficult bit based upon quantum physics light is both a wave and a particle. In a vector examples, light acts only as a particle. So in this diagram light is made up of a stream of particles called photons. With sufficiently sensitive equipment, it can be shown that light, like radiation, is indeed made up of tiny photons.
OK I know this sounds strange. How can it be a wave and a particle but it is……. Yes its hard to get our heads around all this.
Quantum theory is the strange science that deals with very small things (tiny particles), and common sense has seemingly completely contradictory claims. It measures everything in probabilities, the location and velocity of a particle are never known at once (uncertainty principle), every possible universe exists, the cat in the box can be alive and dead at the same time, and a single photon can interfere with itself. It is such an incredible thought that even Einstein, who was involved in the foundations of quantum mechanics anyway, said it was impossible. “God doesn’t play dice,” he said.
An important question. Is light made of particles or is it a wave?
Although light can indeed be detected as a set of particles (photons) (and I talk about it in this descriptor as a particle), it also follows from quantum mechanics that until we observe a given photon exactly, it behaves like a wave, that is, through the optics and all lenses. possible route (these routes will be drawn immediately). It’s his probability wave function that crashes when we observe it (i.e., when he “has to decide” which pixel of your sensor is actually crashing into it).
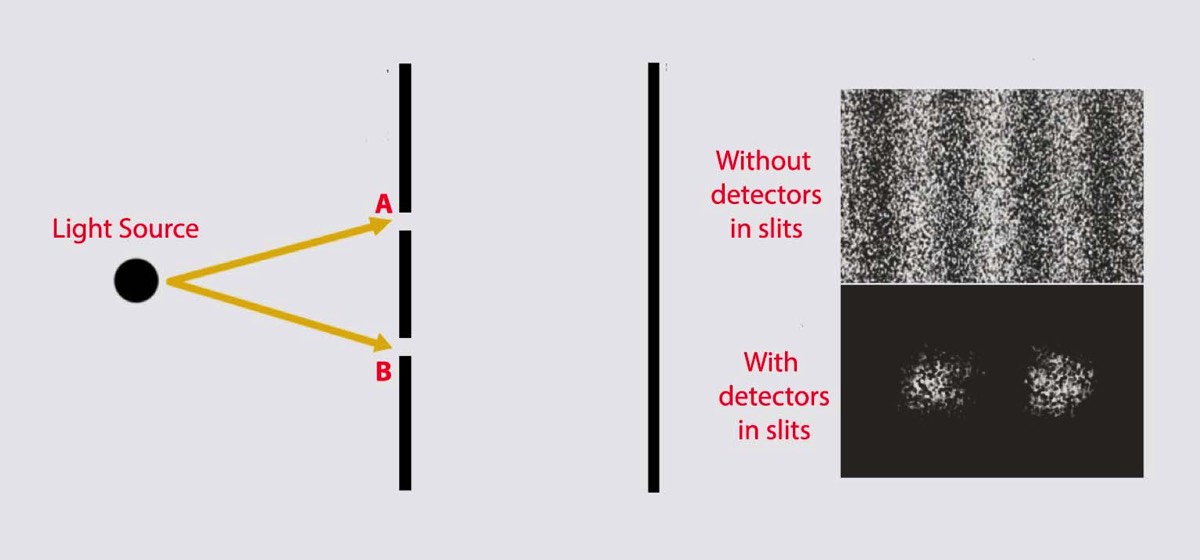
You do not believe it? Yet it is very simple to prove: in the two-slit experiment, a single photon starts towards a plate with only two slits (A, B).
You’d think you had to decide which hole to go through, since no single particle can pass through two holes at once. Well, that's exactly what's happening: a single photon interferes with itself, so you don't see two piles of impact (a pile of photons coming from one or the other) on the screen behind the two slits, but a wave pattern, a typical interference image. Light is clearly a wave.
How the hell is it possible for a single particle to behave like two waves of water when they meet? How can this pattern be created using a single particle?
The shocking thing is that if we place detectors at the two slits, so we observe which slot the photon actually passes through (it stops being a wave and becomes a particle), the wave pattern disappears and indeed two impact zones are created on the screen behind the slits not more. So light is now a particle and not a wave.
In this case, the probability wave function of the photon is collapsed by the observation already at the gaps and "you have to tell" where it actually is. How the photon "knows" when it is observed, when it can be a wave and when it is a particle is not known, but it is probably a matter of our lack of understanding, since light (and very small particles) cannot be perfectly described by an ordinary "wave". Or " particle ".
So God does play dice!
Did I mention how strange the world of quantum mechanics is?
Enough for now let us just focus upon light as a particle to try to understand how a lens works without going totally insane. It is all about simplification to make things at least partly understandable. We are lucky, we have computers and research into quantum mechanics, just think of those early lens designers without all this technology to help!
So if we pretend light is just particles called photons, how can a single photon be detected? Well, believe it or not, the human eye is such a sensitive instrument that it can detect up to 4-5 photons (there are many, many more in normal light), and in the laboratory they use a so-called photoelectron multiplier, which can detect a single photon impact. transforms it into a signal. And the signal is always a unit, that is, it measures either one or more photons, but the number is always an integer. There are no 2.37 photons.
It is important to use monochrome light in the following explanation.
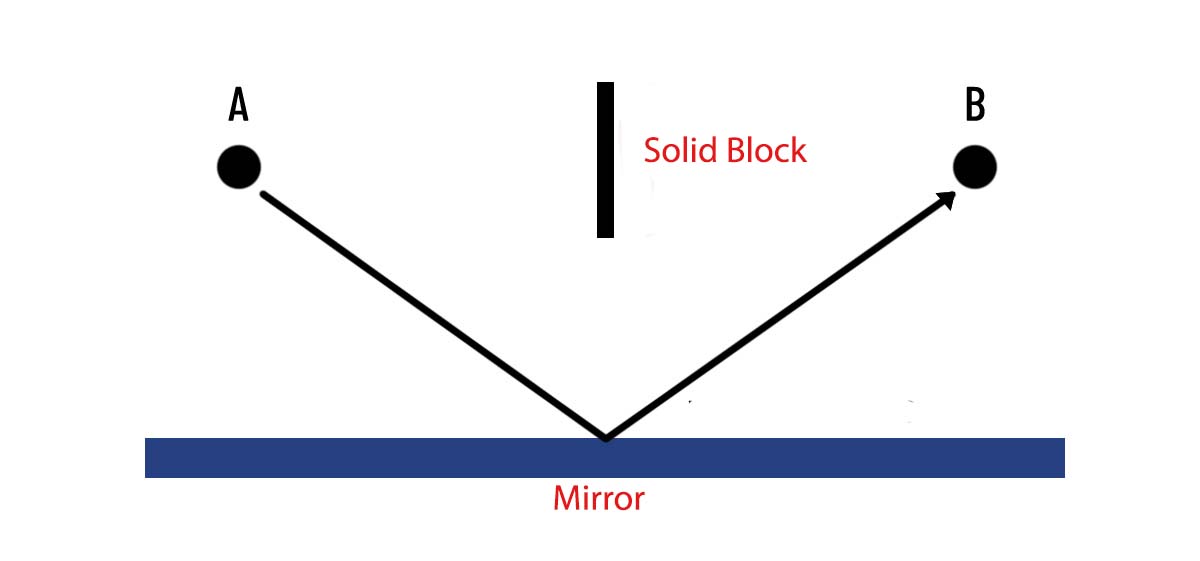
We will place a mirror as shown in the diagram below with a solid block to prevent an easy path from A to B, our past knowledge from school will tell us that the angle of incidence is the same as the angle of reflection, so the photon travels in the following path from point A of emission point to point of arrival B.
But the mirror example is not the case in reality. Quantum mechanics says that light can travel ALL existing paths. No matter how unlikely it may seem. Okay, but where is it really going?
What happens when light hits a mirror.
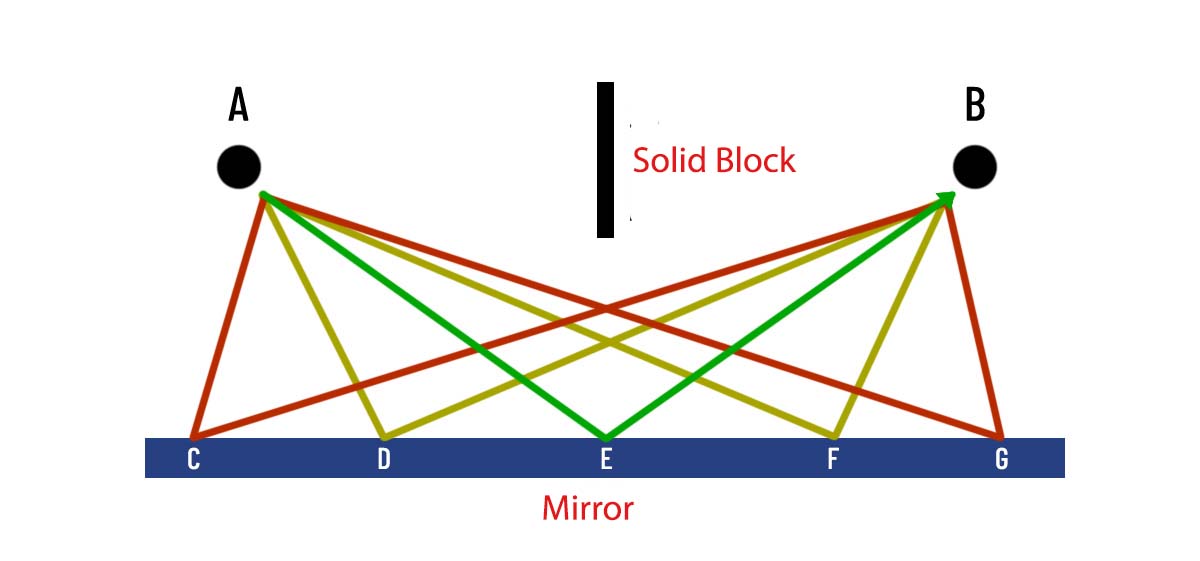
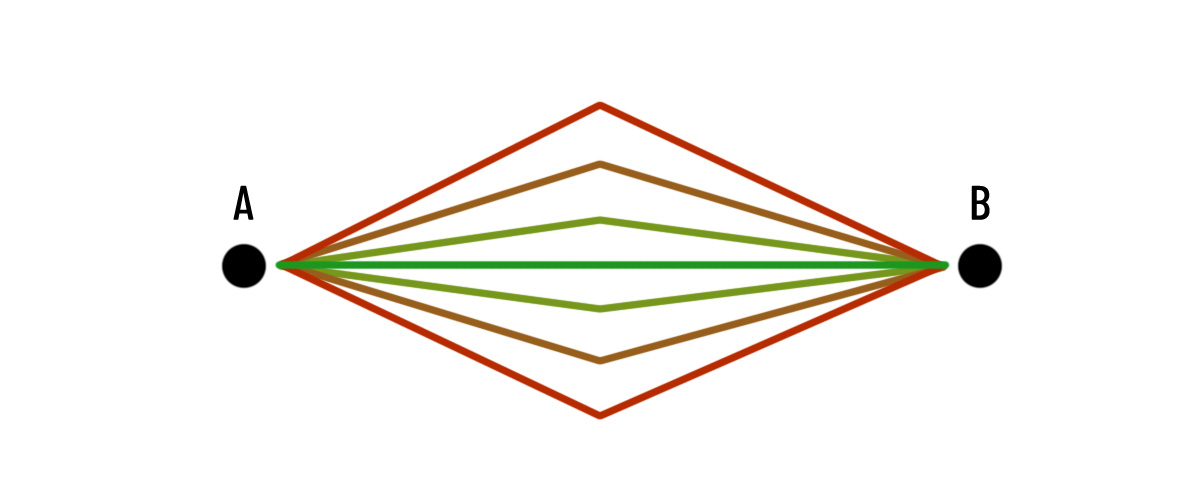
Each trip (different path) will have different durations, as you can see in this figure. Imagine you are running from point A to B the quickest will be the shortest the green line but all routes are possible they just take a little longer. I have used colours here just to show the many possible paths but remember we are looking at black and white NOT diferent colours of light.
Like you would the photon will try to go on the path that takes the least time. Although it could theoretically bounce off the edge of the mirror (by touching points C and G), we see that this means a much longer path overall. If the arrangement is symmetric, we also notice that, if all possible paths were added, the long paths at the two edges (touching C, D, F, and G) would just be less likely in terms of probability.
What remains is in the middle of the mirror, (in time) approx. the sum of journeys of the same length (by touching this point). That is, the light will most likely really go in the middle and the angles of incidence will really be the same as your school knowledge tells you.
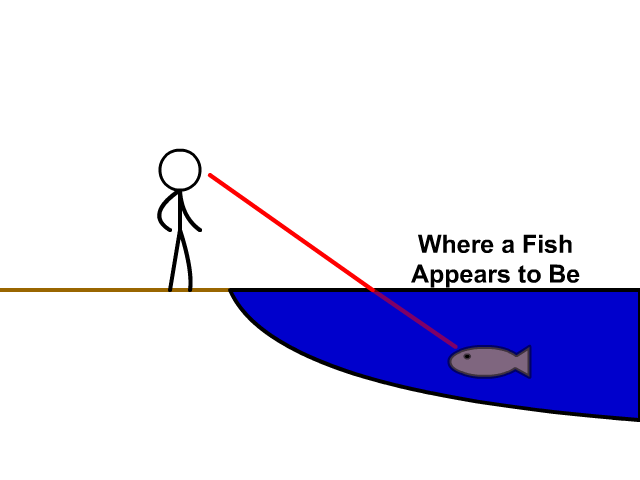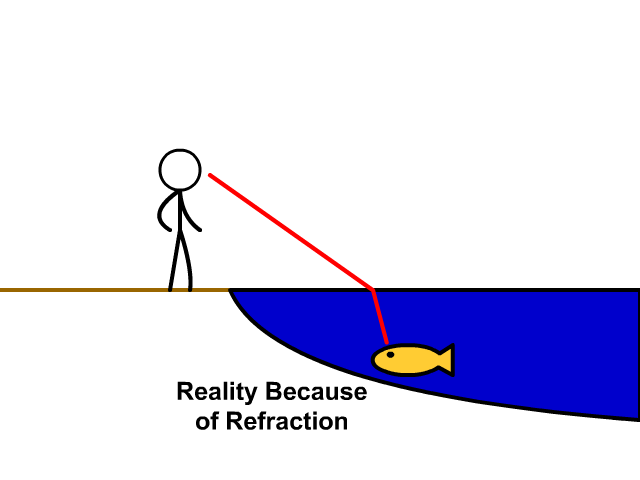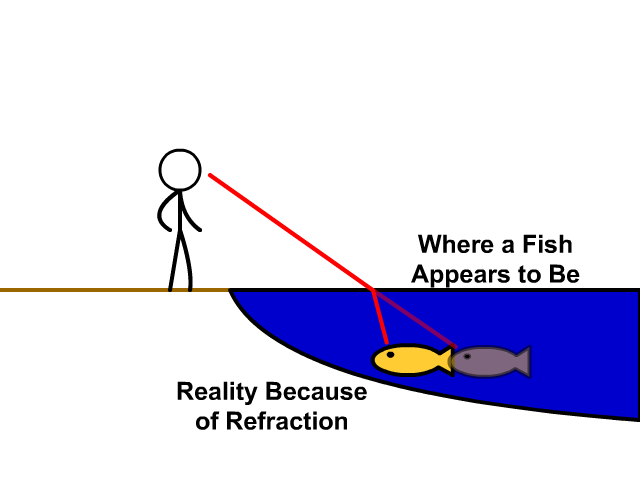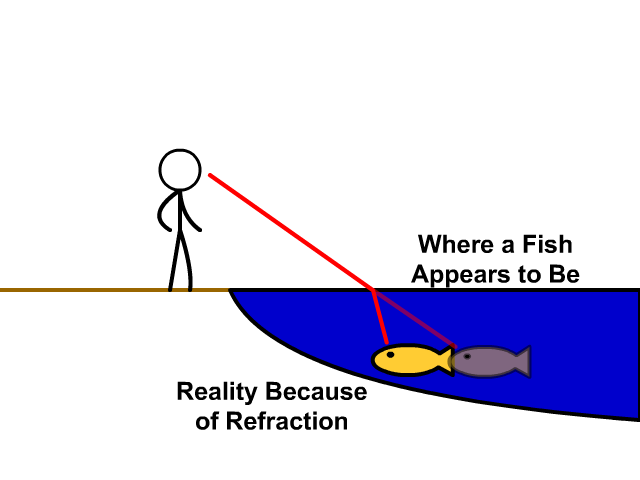
So far so easy. But what if the arrangement is not symmetrical, because the light has to move in different media? You already know, this will be a phenomenon of refraction when you look through water you get a distortion due to the changing media density. If you try and grab something in water you fin it hard to do as the image is detracted.
So refraction occurs and this modifies the path of the light.
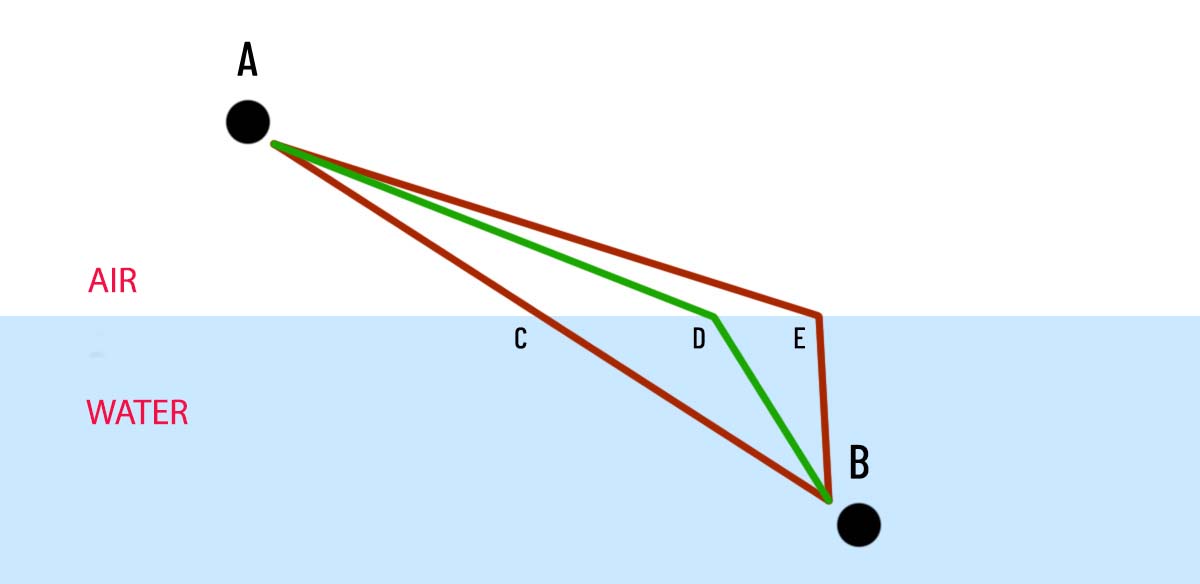
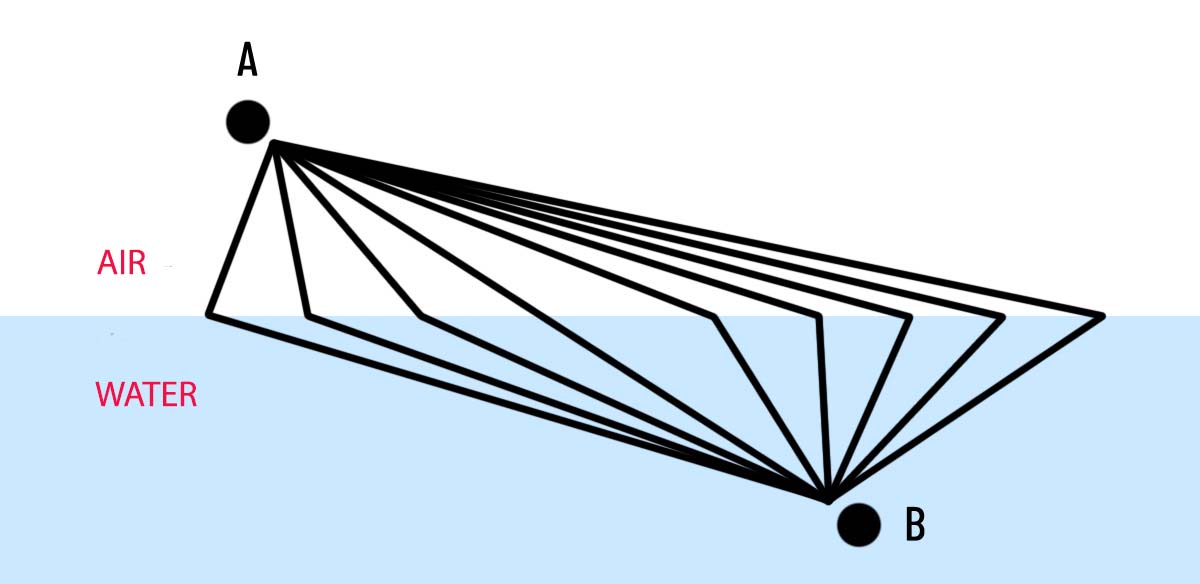
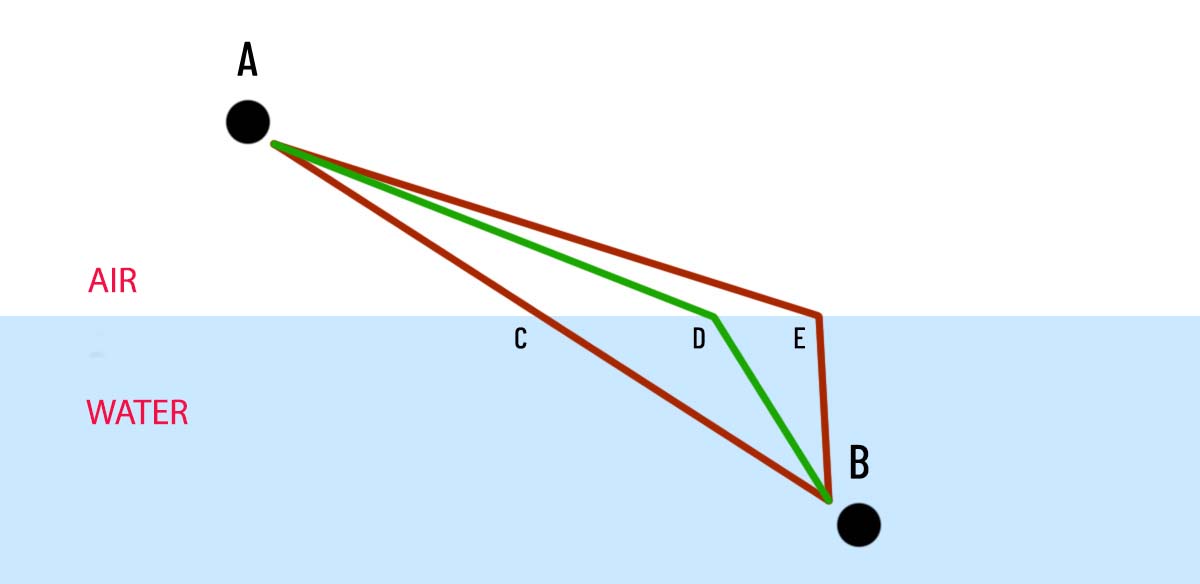
If we use quantum mechanics as a basis we have to draw a radius from point A in the air to point B underwater, I get this (here are just a few paths like the mirror example, but I could draw as many as you like, each with some lesser or greater probability.
Refraction occurs because light travels more slowly in water (and in anything else that is denser than air). So how do you decide which would be the fastest route? It will no longer be a straight line due to the refraction. And why is there refraction anyhow?
If you are running in air you will be faster than trying to run in water, in a room filled with jelly etc. So imaging there is a drowning swimmer: a man (A) on the shore, running much faster than he could run in the water, so he would go in a straight line to the drowning (B), he would run a little further on the shore, so he will have to swim less (which is slower than running). That's how you would get there the fastest.
In this example as glass is denser than air the photon would do the same as the running man the same: it will choose the middle (by touching point D) from the three drawn paths, which, although not the shortest in a straight line (distance) (it would be touching point C), can still travel the fastest on this path.
We can now see that using two materials of different densities, it is possible for the light beam to change the path of the line, so from here it is only a small step to focus the light.
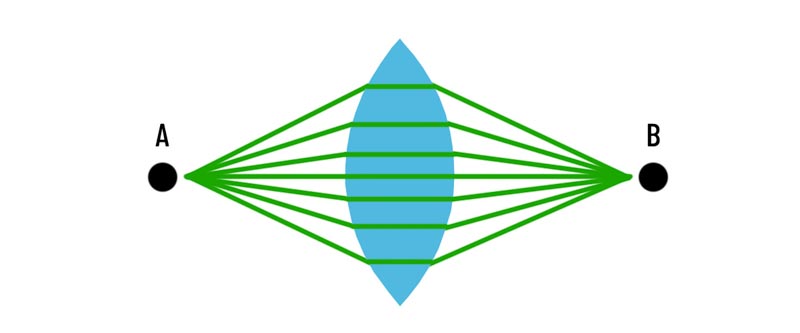
Now let’s see the path of light from A to B again. If I show this in a figure, the photon is much more likely to travel in the middle green paths because it is the shortest time you can travel in time. But in reality we have lots of point A's as we dont have a single beam of light.
But if we add a lens all this changes. All the green lines take the same time to travel. We now have intensified the light at point B. You will know this from setting fire to paper using the sun and a magnifying glass. We take lots of point A's and focus it all on a single point.
All of these paths have the same probability because for the photon, each can walk in the same amount of time due to artificial deceleration.
The condenser lens thus does nothing more than lightly dramatically increase the chances of light rays traveling in different paths meeting at a single point. And when they meet at one point, it means a sharp image on the film / sensor.
Of course not all lenses are convex. But the principle remains the same. Air and glass. Refraction. And photographic lenses contain many combined optical elements.
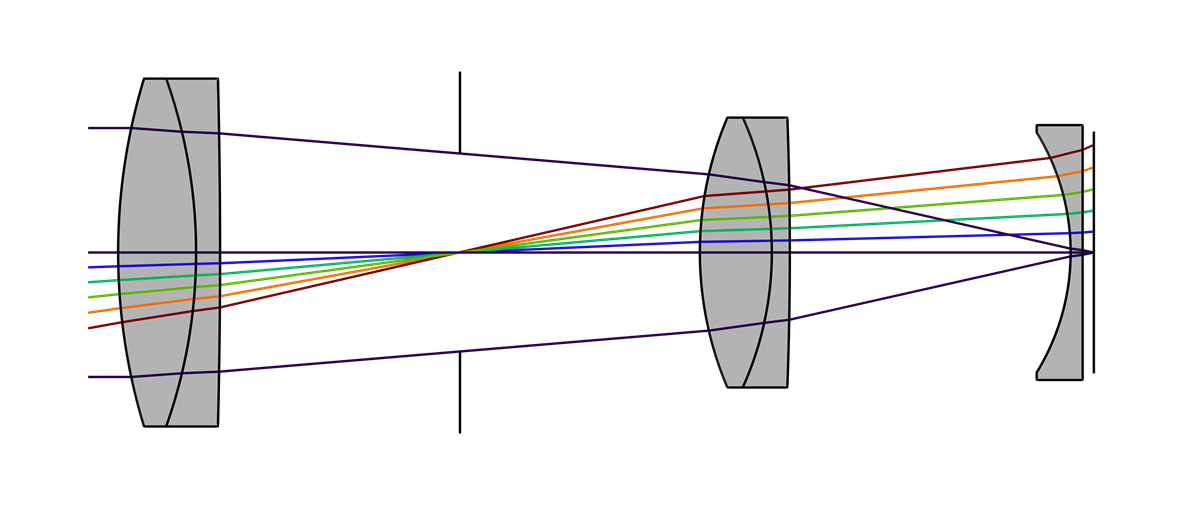
If you pack many different lenses in a row, you can add up all the vectors of the light beam passing through them, so ultimately the whole optics behaves like a single lens. (In fact, the system consists of many lens elements so that all optical indicators are optimal not only in the middle of the image, but also at the edges.)
The situation is complicated by the fact that light rays of different wavelengths, ie different colours, overcome obstacles (lenses) differently, so by the time they exit the system, they are no longer focused in one place. This is a phenomenon of chromatic aberration that causes so many headaches for optics manufacturers. They try to reduce it with lens elements with special geometry.
We have now explained how optics work using quantum electrodynamics. But I am not a physicists. If you’re more interested in all of this, you can read QED: The Strange Theory of Light and Matter.